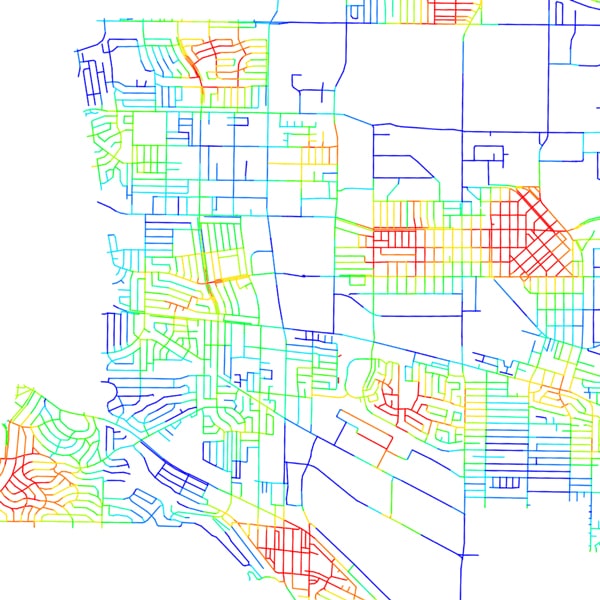
A professional case study in Torrance, California
Introduction
In 2016, we were appointed to study mobility dynamics in the city of Torrance, a city of roughly 100,000-inhabitants located in the County of Los Angeles, 30 km southwest of downtown LA. The main aim of the project was to devise a dissection tool that would allow us to read mobility phenomena in the city of Torrance, understand the city’s mobility needs and ultimately identify a series of pilot projects that would help the city respond adequately to its current and emerging future needs. Moreover, the project was aimed to use the city as a living lab during which a dialogue was meant to be established with public and private stakeholders for testing new models and solutions.
Torrance is part of an urban continuum that, at a first glance, appears to be with consistent similar characteristics – low to medium densities, similar grid structures, car dependency, etc. All this is true (to a certain extent), nevertheless, once census traits are looked at in more detail, another layer of complexity starts to be revealed, unveiling microscopic differences that represent the intrinsic qualities of Los Angeles’s multipolar urban reality. Here we see a fragmented territory caused and demarcated, on the one hand, by the very basic geometric administrative boundaries and fragments imposed on it since its constitution and, on the other hand, by deeply rooted inequalities, such as varying crime levels, income levels, public transport coverage and several other features. This made any effort to analyze and understand any given part of the whole, without taking into due consideration its relationship to the entire system, a futile one.
Therefore, one of the main reasons why Space Syntax was explored was to establish a cross-scale reading between analyzing the part, the whole and the relations therein, with the aim of scientifically tying abstract spatial relationships and specific block traits and characteristics. Moreover, the complex and open-ended objective of this study pushed us to seek analytical instruments that go beyond the traditional trades and explore multi-fold readings in the endeavor to link between scales, urban grids, network extensions, agglomerations, etc. hence reading the territory in a continuous manner, unaffected by the aforementioned spatial divisions and intrinsic socio-economic differences.
Space Syntax (SSx) was used principally for the following reasons:
SSx is capable of establishing relationships on different scales among parts of the network and their relationship to the whole.
SSx establishes a scale on which the strength of relationships between networks, adjacent or remote, can be established, read and analyzed.
SSx is a universal algorithm that is capable of establishing comparisons among different network shapes in different cities.
SSx provides graphical output that is useful in formulating immediate observations, as well as numerical outputs that can be compared against other numerical data, such as traffic volumes, speeds, etc.
SSx is used for carrying out correlation exercises that, if well-developed, may provide grounds for predictive methods for other projects.
The results obtained from Space Syntax proved to be beneficial in multiple aspects in achieving our project objectives and in tailor-making our proposed interventions and pilot projects. Findings reflected on network clusters and network characteristics, opening up debate on how to connect different parts of the urban continuum while overcoming governance and socio-demographic obstacles embedded within the LA territory. Furthermore, space syntax mapping findings contributed to giving a ‘scale’ to the typology of interventions that were aimed at improving walkability conditions and in devising the appropriate offerings for shifting transit towards greener and more active modalities.
1.1. Mean Depth Analysis: Reinforcing network clusters
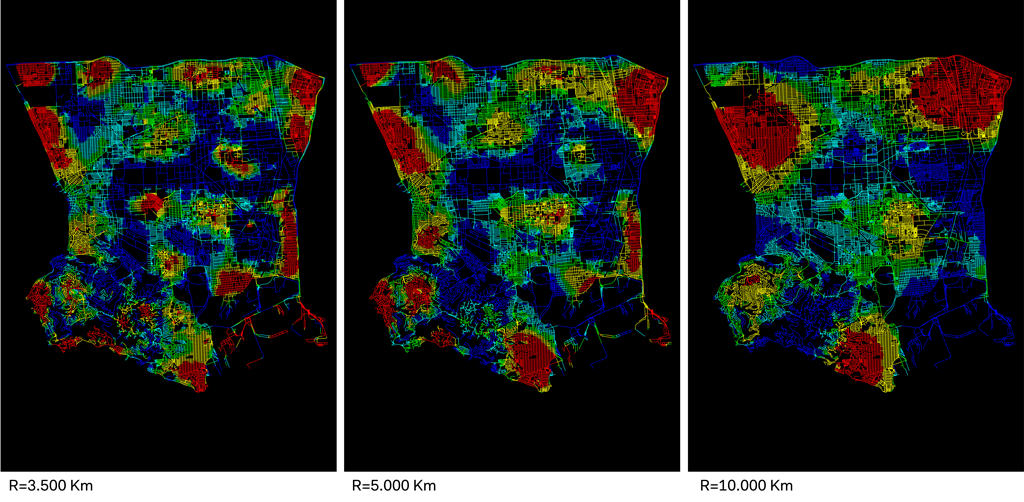
The Mean Depth Analysis, shown in detail later in this paper, had led to interesting results that benefited the entire study. This exercise, carried out on a wide area scale, covering a total area of roughly 500 sq-km and stretching from the southern fringes of Los Angeles International Airport to the eastern side of Long Beach, indicated the minimum radius at which network clusters start to form. At a radius of 1.6 km Old Town Torrance formed independently a cluster similar to other networks, such as El Segundo, Manhattan beach, Lennox and several others. Carrying out the same test while gradually increasing the radius allowed us to identify the threshold at which the network in Old Town Torrance started to become ‘weaker’ when compared to other much more consolidated and extended network clusters, such as Manhattan Beach, East Compton and a few others.
1.2. Choice Analysis: Shifting transit modes
One of the main project objectives was to improve walkability conditions, increase sense of community and seek network improvements in order to shift transit choice towards greener and more active modalities. In addition to the consolidated analytical planning tools that we used in this exercise, such as the Pedestrian Level of Service, Walk Score and the National Walkability Index, we needed to look into the degree to which the intrinsic morphological qualities of a network can influence transit mode choice and curb or encourage movement by foot, or by any similar non-motorized modes such as scooters, bicycles, and other personal devices.
To this end, the network choice (betweenness) was used to identify those streets that form part of the shortest trip from all origins to all destinations. As high choice scores indicate a high potential for ‘through’ movements, the streets with highest scores were identified as streets that are inherently important parts of many journeys (Turner, 2007). The reason for which the comparative exercise that we carried out settled on comparing Torrance to Milan was basically the radically distinct form and nature of the two cities. Milan is a radial and center-based city which central part replicates a medieval organic structure surrounded by a series of ring roads that were built in different eras with grid structures that vary at every ring, as it was influenced by the era of its construction.
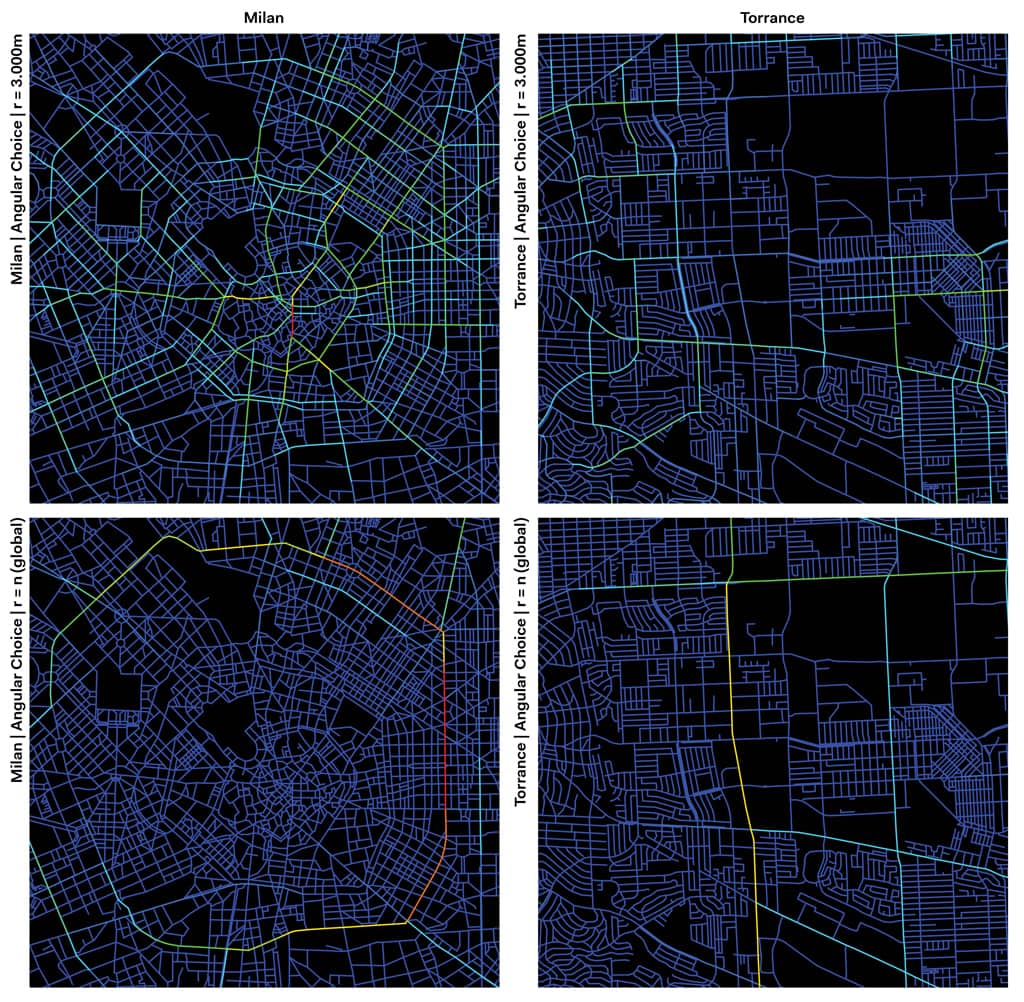
Figure 02 – Segment analysis – angular choice comparison between Torrance and Milan
1.3. Paper Structure
This paper is divided in three parts which address three different consecutive analytical exercises that were carried for the city of Torrance: in Part 1 we performed typical spatial analysis to explore Torrance’s structure; in Part 2 the correlation between Space Syntax output and traffic flows is assessed; in Part 3 different types of micro-centralities are defined based on the previous studies, in order to drive the decision-making process of the transport strategies. Results of each study is shown and detailed within each specific chapter, while conclusions and next steps ahead are summarized in the final chapter.
PART 1: Network Analysis
Our project appointment to conduct a general mobility study in Torrance was largely open ended, setting two standards for our project. First, as there were no specific ‘problems’ or constraints identified, we exploited this flexibility to experiment and seek alternative readings of the transport network as a whole, as well as the embedded relationships within it, with the aim of identifying potential mobility interventions in the city and pave the way for future applications on other projects. The second standard for our work again stems from, and anchors on, the flexibility provided for setting the methodology and outcome completely autonomously. We decided that the best way to start exploring the urban form in Torrance and setting our own project goals and constraints would be through the use of space syntax analytical tools. Further, there would be an opportunity to employ a more novel approach and demonstrate the value of the approach through our work. This was aimed to open up for a multi-disciplinary platform for discussion and tests in finding new correlations through merging the professional lenses of architects, engineers and urban planners involved in this project. Therefore, not having the time, financial, nor specific client demands imposing constraints on our project or workflow, as is usually common in our daily professional practice, we were left with the conditions of opening up and testing unprecedented approaches both in our own approach and in the field of mobility analytics as a whole.
In the early stages of a city or region-wide analysis, observational analysis is often sufficient to start recognising patterns in the urban form and street structures; neighbourhood and district centres can be identified, as well as historical or significant street connections between these places. Some gradation of density and desirable or less desirable places can usually be intuitively understood, especially by trained practitioners. However, in Torrance, perhaps representative of certain North American cities, this is not the case. The city grids and their confines are largely ‘blurry’ and ‘continuous’ meaning that by observation, there are very few structural patterns which could be outright identified:
there is almost no variation in density
apart from ‘Old Town’ Torrance there are no recognizable neighbourhood units
significant streets cannot be identified by observation alone. The 800m grid system repeats almost indefinitely, either ‘filled-in’ with lollipop-style suburban development, simple grid structure, or private gated communities
commerce and retail are relegated to seemingly random main street intersections, giant shopping complexes, or dispersed in the Old Town
Of course, this is not to say that it is impossible to read the city form or observe certain patterns. However, this pervasive ‘continuum’ of the city is unusual and challenging to deal with, especially when approaching from a European urban perspective, and further demonstrates the applicability and necessity of spatial analysis. We therefore determined that the best way to commence and direct our analyses would be through a comprehensive application of space syntax to highlight and identify patterns in the city form that are otherwise too complex for mere observations.
2.1. Comprehensive Spatial Analysis
Considering the morphological and spatial structure of Torrance, we decided against applying axial analysis for two reasons. First, many streets continue perfectly straight almost indefinitely, which would result in axial lines beyond 10km, obviously subverting the notion that axiality generally corresponds with lines of site as formed by an urban environment or degree of enclosure, as well as the intuitive movement decision-making associated with this perception of the urban form. Second, we needed an analysis capable of driving the decision-making process for a variety of transport solutions at different radii, from small-range pedestrian relations, to medium-range cycling movements and long-range vehicular movements. For these reasons, we could justify our use of segment analysis instead of axial analysis (Turner, 2007).
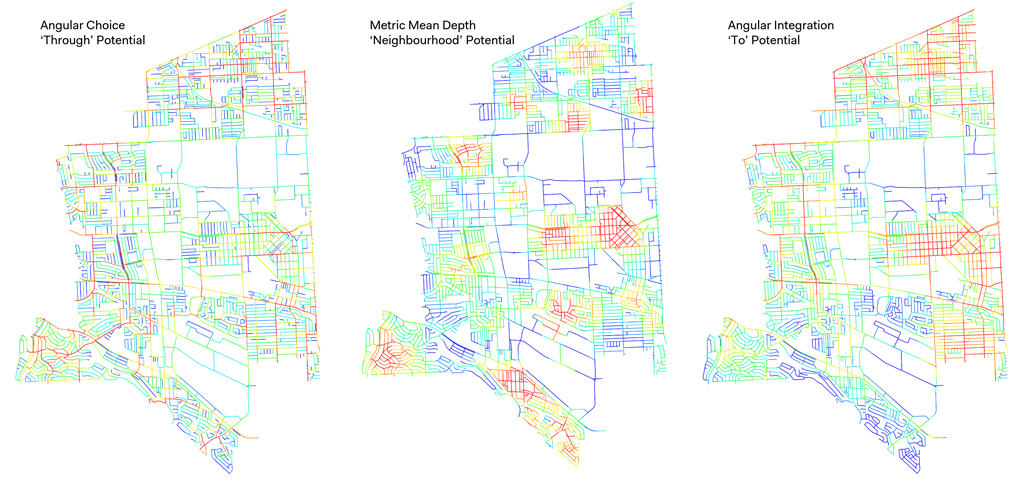
Figure 03 – Angular Global Integration
A segment map was created from centerline data that was manipulated by hand to remove double lines on boulevards, simplify highways to single line representations, remove lanes and service ways, etc. The segment map covers the entirety of the city and an arbitrary contextual area spanning an area of southwest Los Angeles approximately 4 times the size of the city alone. All analyses were conducted at metric radii of 200m, 400, 800, 1200, 1600, 2000, 2500, 3000, 3500, 5000, 7500, 10.000, 15.000, 20.000, and n. We examined 5 syntactical studies: Angular Integration, Angular Choice, Metric Integration, Metric Choice, and Metric Mean Depth. The metric radii were chosen to represent thresholds corresponding to walking distances (400, 800, 1200) and then other logical radii with sensible differences as opposed to 100m, 200m, 300m, etc. The decision to study angular and metric measures was not based on any prior experience, nor academic discourse, but rather to be concise and to have the information to later determine which measures held the most meaningful information about the city’s spatial structure.
We do not intend to report the nuances of our spatial analysis in Torrance, but instead we may recapitulate the key observations with a focus on how these findings were interpreted to feed into the larger professional mobility study, inform our teamwork, and direct the next steps in the project. We record the 4 most interesting observations:
For each analytical type, there was a clear-cut threshold between the radii at which no centrality patterns could be detected, when the centrality patterns reflecting local structures, and when the patterns reflected large-scale movement patterns. In other words, the centrality ‘core’ (top 10-20%) at lower radii did not show any emerging patterns, at mid-scale radii, centralities often reflected neighborhood structures, and at larger radii concentrated on the streets designed for long-distance movement. Interestingly there was almost no overlap between these categories: if a street was significant at a lower radius then beyond this threshold it was no longer significant.
The ‘continuum’ that characterizes Torrance is reflected in its grid structure. Both by observation and through the centrality analyses, the prevailing grid structure is clear, with little variation in centrality between the streets forming the grids. While it might be expected that certain routes would be more significant in the spatial structure, this was not the case with each major North/ South gridline holding similar centrality values.
Metric Mean Depth proved to coincide with the region’s neighborhoods in Old Town Torrance, Manhattan Beach, Lincoln Village, and other neighborhoods named on any map. However, these patterns did not emerge until larger radii (>1600m) suggesting that the notion of a neighborhood in Southwest Los Angeles may not walkable or at a ‘human-scale’.
We would normally expect that a measure of global integration would reflect some sort of geometric center of the network. Instead, in Torrance and our study area, angular global integration demonstrates the pervasive centrality of the major N/S and E/W routes (see figure 03 – right). Even these segments geometrically and geographically distant from the center of the network still demonstrate high global integration, which is quite unusual in centrality analyses of the urban form. In terms of urban design and mobility factors, this reflects that the city is not as much characterized by ‘place’ as much as it is on movement between ‘places’. This was one of the most revealing findings of the preliminary analyses as it reflects both the ideology behind the mobility design of a place like Torrance, as much as the character and lifestyle of the place.
2.2. Torrance v. Milan Comparison
This preliminary analysis using space syntax gave us valuable insight into how Torrance worked and importantly, how people moved through the area. We observed how neighborhoods were formed and connected, and how patterns of central streets emerged and changed considering different radii and hence scales of movement. While we could use this information to start dissecting the otherwise difficult to read urban ‘continuum’ that is Torrance, we still lacked a contextual understanding. We therefore employed a comparison of the spatial patterns in Milan, where our team is based, a city we know intimately, and a standard example of European building practices. The segment map was derived for Milan with the same standards of simplification, and the same centrality analyses were processed. Normalized Angular Integration (NAIN) and Choice (NACH) were also computed for both Torrance and Milan for the direct quantitative comparison between the two cities (Hillier, Yang, Turner, 2012).
First, a visual observation was made between the two cities, comparing integration, choice, and mean depth at the same scales and with the same interval classifications. The top 10% core was visualized to directly understand which were the most important streets for each analysis and scale. The visual observations were immediately valuable, demonstrating key differences between a more compact, traditional, and ‘mobile’ (walkable, cyclable, good public transport, etc.) urban structure with a typical North American car-dominated sprawling metropolis. Then, NAIN and NACH values were used for a quantitative comparison tracking the average values in the cities at the various radii as a means of determining which place was more integrated or demonstrated higher choice value at the various scales.
Again, we will not dwell on the nuances of our observations, but three key findings are reported. Like the discussion of Torrance, we feel that these findings reflect our perceptions of space syntax as mobility analysts and who are using this analysis to provide a context for a larger study as opposed to focusing on network centrality as the exclusive driver of our work.
In Torrance we saw no significant patterns of centrality emerge at smaller scales. However, in Milan we could detect patterns emerging already at 400m across all analyses. These patterns are meaningful and coincide with patterns we already know of retail allocation, movement channels, and historical significance. From this, we can corroborate our initial thoughts that in Torrance there are few structures reflecting any sort of movement conducive to walking and that it is not just theoretically built to prioritize the car, but that the scale and street structures also reflect this ideology.
Metric Mean Depth in both cities identified neighborhood structures. In Milan, we saw that these neighborhoods ‘grew’ when looking at incrementally larger radii, ultimately connecting and merging at larger scales. This reflects what we know about the city, where small neighborhoods may be identified as such and have unique characters, but become part of larger zones when we consider successively larger urban scales. Whereas the neighborhoods identified through Metric Mean Depth (MMD) in Torrance at smaller scales were often not part of the larger MMD clusters at larger scales, indicating that these neighborhoods are structurally independent. Simply, Milan is a city comprised of individual neighborhoods whereas in Torrance this is not the case.
Figure 04 shows that on smaller radii, Milan has overall higher integration values, but at larger radii Torrance has higher integration values. At r = 5.000m there is no statistical difference between the mean NAIN values (as verified by Analysis of Variance (ANOVA) tests). This indicates that the structure of Milan may be more conducive to walking and cycling, whereas in Torrance the structure is more conducive to longer trips. In regards to NACH, Milan has higher Choice values than in Torrance at all scales except 400m. This may indicate the streets in Milan naturally each form a part of more shortest-distance trips than in Torrance. We interpret this as signifying that there are more movement alternatives in Milan than in Torrance.
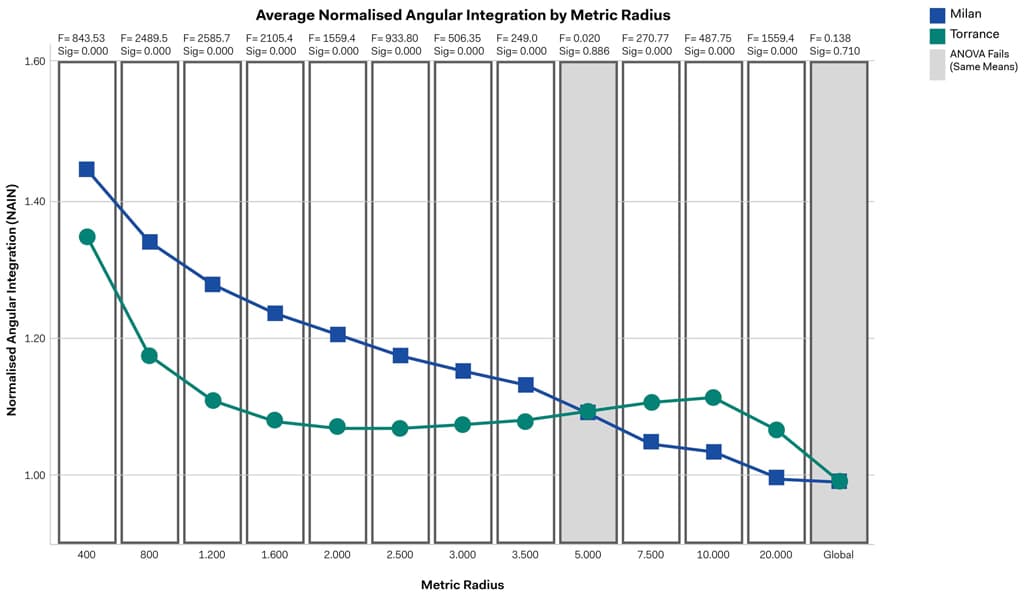
In summary, we applied space syntax to begin to recognize patterns in the urban form of Torrance, in particular in those movement structures of the city that are at the core of our work. The results proved interesting, gave us direction, and also provided strong insight at this phase in the project, however lacked a contextual basis. To make an interesting comparison, one that we could relate to, and one that would immediately highlight the vast differences between a place like Torrance and a recognizably walkable, compact, and public-transport oriented European city, we employed a cross comparison between Milan and Torrance. Visual observations were made on the same radii and same analyses, and a quantitative comparison of average NAIN and NACH were used to confirm which city as more integrated or more between overall. This comparison confirmed many of our initial observations in Torrance regarding scales of movement and neighborhood patterns.
PART 2: Correlation with traffic data
The second application of space syntax in our mobility study for Torrance was in the analysis of traffic volumes. Particularly, we wanted to understand if traffic flows in the city responded to spatial patterns, to what extent, why, and if not, why not. Although this could easily be expanded to also study counts of pedestrians (as with traditional applications of space syntax) and bicyclists, this information was not available to us and was beyond the scope of the project to measure these counts manually. The available traffic data was attached to the segment map in Torrance that was used for the preliminary analyses discussed in Section 2.
Our first step was to explore the correlation between the various centrality measures we had previously computed and three dimensions of traffic movement and design: flow, speed limits, and lane counts. On first thought, studying the correlations between centrality measurements and speed limits and lanes counts seems unusual; we believe that even these non-structural aspects of the movement network still reflect an intuitive relationship with street hierarchies and use, especially at higher level planning scales, and we determined it was valuable to examine these relationships.
We employed the standard Pearson Product Moment Correlation Coefficient to assess these correlations and the results are shown in Figure 05. In the case of Metric Choice, we see a consistent and pervasive positive correlation between metric radii and traffic volume, speed limits, and average number of lanes. These correlations are not extremely high (around .50) however are statistically valid and strong enough to accept as meaningful. At this point, we were confident to confirm that there is a relationship between road design, desired movement, and actual traffic flows with metric choice. This is quite consistent with the results of the preliminary analysis, that the spatial structure in Torrance is conducive to movement by the vehicle. A correlation with metric choice makes sense; drivers make decisions based on sheer distance, not necessarily on turning cost, particularly in a grid system.
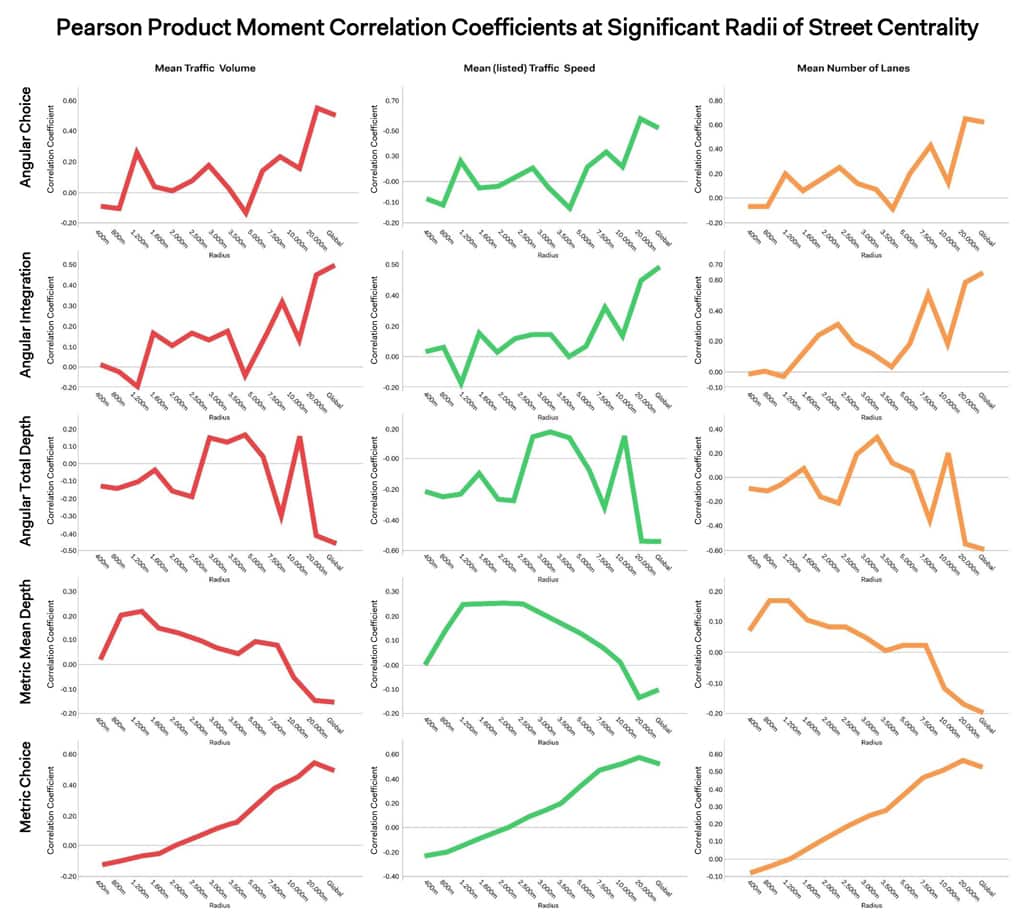
While we observe these correlations and can explain these patterns between traffic and centrality, we must not forget that correlation measures do not imply causation — we cannot say that there is traffic on a particular street because it is a highly central one. However, we can also say that, based on common understanding, a street does not become central because there is a lot of traffic on it, but rather because of its role in the overall system. Therefore, we are confident in assuming, and also for professional purposes, that there is some influence of the naturally forming street centralities in guiding and influencing the emerging traffic patterns.
The next step was to accompany the correlation analyses with scatter plots and compute the linear regression between vehicles per hour (flow) and segment centrality. The purpose of this step was to further investigate how and why traffic orients itself in the city, in relation to spatial properties of the streets. One relevant observation was the fact that there are many instances of high traffic flows on non-central streets. The logical assumption is that these streets might be the shortcuts that are used in the city, perhaps by drivers who want to avoid the congested highways and primary streets or that unintentionally shorten normal trips by cutting through neighborhoods.
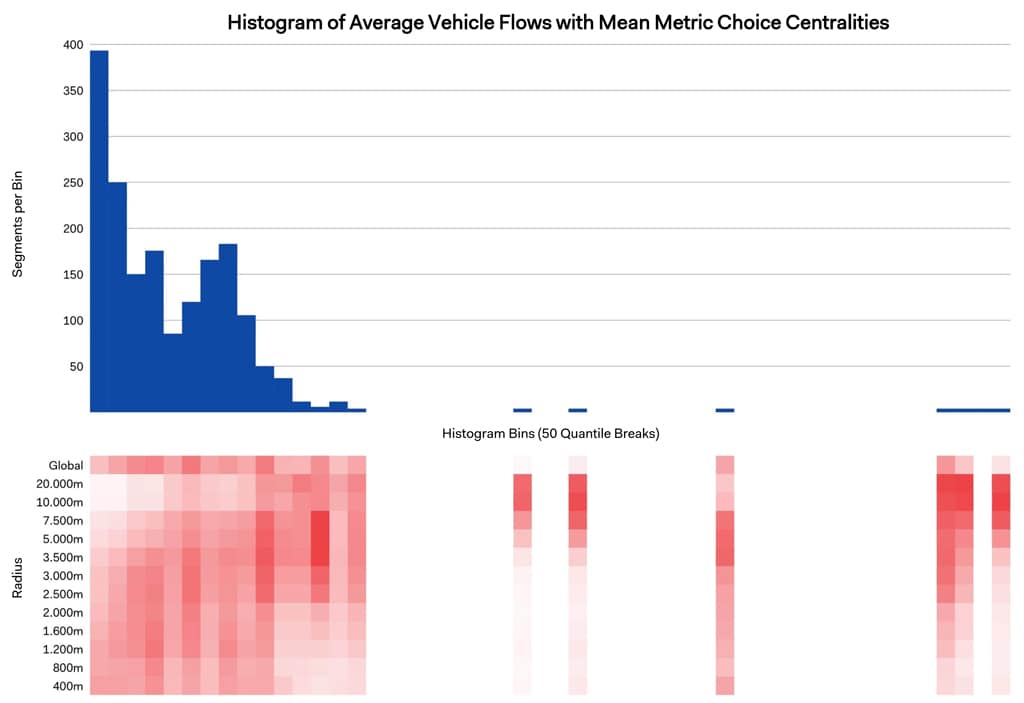
To further investigate the actual distribution of traffic flows on streets with different centralities, we created a histogram showing the number of streets (segments) which hosted a specific range of traffic flows. The histogram demonstrates a strong skew to the left, meaning that there are disproportionately more segments with low flows than with high flows; this is to be expected. We also observed that the fewer streets with higher flows also had more significant metric choice values at higher radii, whereas the streets with low traffic flows did not have significant metric choice values at lower radii. This begs the question whether there is any sort of separation between local and global traffic flows, or if all traffic simply follows the most central streets for various distances depending on trip length.
This question was important to us as mobility analysts, and remained a theme in the duration of the project. Perhaps these streets are simply perceived as the best routes because they are long, straight, and connect the various sanctuary areas (Dibble, 2017) of the city. Or perhaps drivers are naturally inclined to take trips to other parts of the city using the ‘main’ streets as opposed to local neighborhood streets. Or also likely, drivers naturally prefer to move faster in their vehicles, sometimes even if that means taking trips that are actually longer it is more comfortable to move at higher speeds and with less interruptions from stop signs, less risk of a child moving in front of the car, etc.
In the previous studies we have discussed the relationship (correlation) between traffic flows and metric choice centralities. We have made observations and begun to understand these findings in the context of larger mobility patterns and behaviors, and asked questions that have set a tone for the further development of our strategies and subsequent analyses. The final investigation in this component of our greater mobility study is by considering the relationship between centrality and traffic flows on subsets of the street network. These subsets are defined by the assigned street hierarchy according to the city of Torrance. In order, the city of Torrance defines streets as Freeways, Highways, Primary Streets, Secondary Streets, and Other Streets.
The methodology established determined a ‘predicted’ traffic flow on each street (segment) in Torrance, which was based on a redistribution of overall observed traffic flows to correspond with metric choice centrality. Flows were distributed such that the observed maximum flow was reassigned to the segment with the highest metric choice at each radius, the minimum observed flow was reassigned to the segment with the minimal metric choice, and for each other segment the flows were linearly redistributed to follow the distribution of centrality values. From this we produced ‘predicted’ traffic flows for all streets at all radii. To determine which ‘predicted’ distribution of traffic was the most similar to the observed distribution of traffic, we employed Gower’s Coefficient of Overall Similarity (Gower, 1971) to produce a coefficient between 0 and 1, where 1 would represent identical systems.
The similarity coefficient was calculated considering:
All streets in Torrance
Freeways
Highways
Primary Streets
Secondary Streets
Other Streets
Figure 07 reports the coefficients of similar computed at each radius in each of the 6 scenarios listed above, and highlighted from least similar (red) to most similar (green).
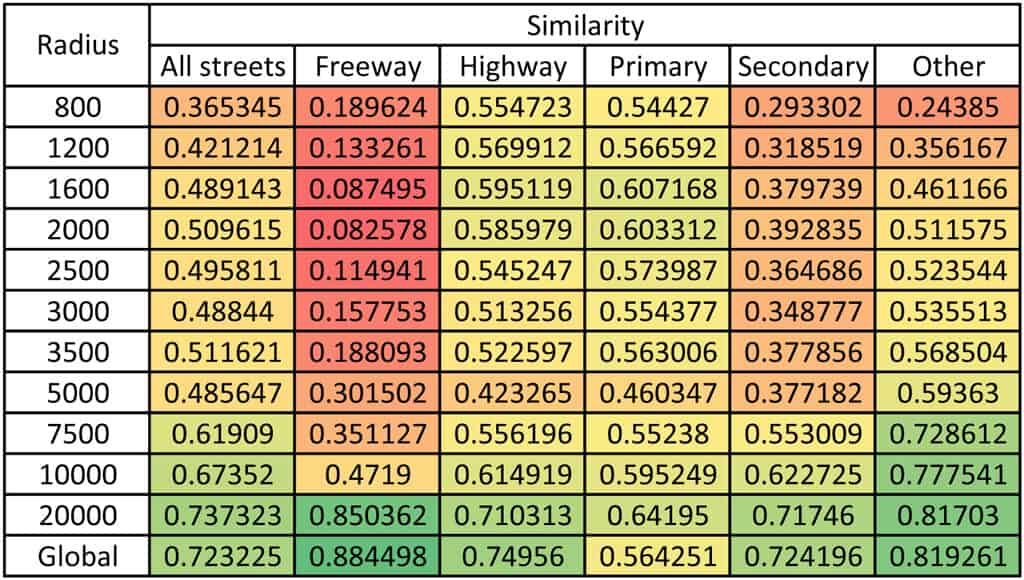
In all cases except for the scenario considering exclusively Primary Streets, the predicted traffic flows based on Global Metric Choice show the highest overall similarity with the observed traffic flows. Further, these are all statistically significant (r2 < .05) measures and represent very strong positive correlations with p > .72 in all cases. In the Primary Streets Scenario, the predicted traffic flows at radius 20.000m are the most similar to the observed traffic flows. Visual observation concluded that r = 20.000m and r = n are highly similar, and a correlation between the two systems showed a .95 relationship; this is sufficient to conclude that for this study, r = 20.000 and r = n are one in the same.
In all cases, we confirm that the ‘predicted’ traffic flows based on global metric choice centrality is the most similar to the actual traffic flows in Torrance. So, if the observed traffic best follows that which would be predicted if all motorists follow the most globally central streets, what does this tell us? This raises TWO questions:
Does some of the traffic actually follow streets that are central at lower radii and the rest of it follows streets central at a higher radii, and the overall correlation with global routes is simply an ‘averaging out’ of the results?
Does the spatial structure and morphology in Torrance encourage motorists to simply join the fastest, widest, straightest streets which as we verified earlier in this section, are also the most central? In other words, do motorists drive on the fastest streets regardless of their trip distance?
We did not answer these questions, but rather used them to guide the further development of our analysis and methodologies, and to develop an appropriate strategy in Torrance. An interesting observation is that when we consider the scenarios of Secondary Streets and Other Streets, we still see that observed traffic follows predominantly Global predictions, therefore being used for global movement in Torrance. This inconsistency also raises important questions that have helped us in developing further strategies for Torrance:
Can this be verified further, if local streets are being used for global movement?
Is this desirable? Do we want traffic to naturally find the best way of moving, or do we want neighborhood streets to be calm, quiet, and safe for children?
To what extent can we manipulate traffic flows through street design, public transport, or other interventions?
In summary, we used space syntax as a method of understanding how and why traffic flows occur in Torrance, by exploring the relationships between traffic and centrality. We found that traffic correlates (consistently, but not strongly) with metric choice values. Further analyses revealed that the streets (segments) with lower traffic volumes generally were not central at any radius, although the streets with higher traffic volumes were central at larger radii. A novel methodology comparing predicted traffic flows based on metric choice with observed traffic flows indicates that all streets in Torrance are generally used for global movement patterns, an inconsistency that will influence further strategic development in our mobility study.
PART 3: Identification of micro-centralities
The third application of space syntax in the mobility study for Torrance was in the development of a strategy for further works and interventions, looking both at punctual interventions (e.g. implementation of bike sharing stations, electric vehicles charging stations, bus stops, etc.) and linear types of projects (e.g. new cycle lanes, bus routes, etc.). Instead of focusing immediately on the definition of the strategies, like it is normally done, we rather created a guideline to ensure that any subsequent projects in the city were mobility-focused. Thus, we developed a succinct ‘Micro-centre Strategy’ based on network centrality criteria and our ideas for valid starting points for mobility interventions of various scales in and around Torrance.
The strategy we developed needed to be relevant in the future regardless of the type of intervention or project; if the city determines shared bicycles are the best solution to a future problem, then the micro-centre strategy should be relevant. Equally, if the city wants to explore driverless vehicles, new construction, total regeneration, or any public transportation intervention, the strategy should still be relevant. We naturally thought that we then need to develop a strategy focusing on stationary locations as well as movement, and that is relevant both on large and small scales. The idea then become to identify local centres, or micro-centres, and determine a strategy to connect them that would be relevant for interventions and particularly, mobility solutions at both small and large scales.
4.1. Stationary Centres
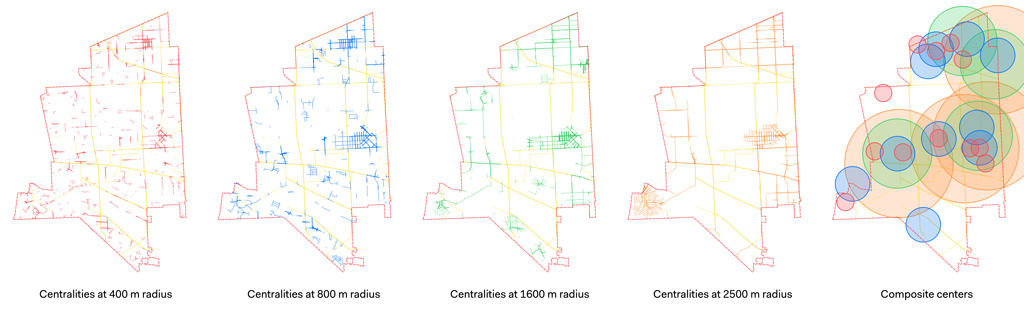
For any type of use in future projects, we needed to identify the centres in the city that are the most ‘central’ on a variety of criteria. In a more standard project, the intuition would be to choose centres based on points of interest and existing infrastructure, but we instead chose to principles of spatial centrality to determine the most natural central locations. At various radii, the top 10% Angular Choice, Angular Integration, and Metric Mean Depth maps were computed and overlaid. These three measures were chosen based on our findings in the prior analyses and in the strong representation of the spatial character of Torrance and its environs. The top 10% segments for each measurement were overlaid on the map, and any segment present in all three top sub-sets was selected. This left a series of disconnected ‘islands’ in the map. The midpoints (along the paths) of these disconnected islands were identified and became the static point/ centre for that particular radius. Radii considered were 400m, 800, 1600, and 2500 to consider those segments most significant for 5 and 10-minute walks, district level distribution of existing amenities, and the maximum distance to expect a bicyclist to travel for a non-commuter trip.
4.2. Connections
The resulting map is shown in figure 09 and shows the selection of micro-centres. The second facet of the development of this strategy was deriving a means for connecting these centres, providing the basis for the transport strategies. Our first intuition was to examine the core centrality networks at various scales; for example, the most logical connection between 400m Integration/ Choice/ Metric Mean Depth centres would potentially be the streets with the highest 400m choice values, and so on.
However, this would result in essentially 4 networks being used as theoretical connections between these micro-centres. We determined it would be more sensible to determine a single network to focus any future efforts on. This network was chosen as the intersection between the top 10% of Global Metric choice streets and the top 10% of Global Metric Integration. These are then the streets with the greatest ‘to’ and ‘through’ potential at the scale of the entire city, and give the best single network to connect the micro-centres at various scales. Our previous analysis suggested that vehicular flows follow Metric Choice; considering that the private vehicle is and will be the preferred choice of transit in the Los Angeles area into the future, it is appropriate to consider metric computations for our strategies.
While in Section 2 we listed the 5 classifications of streets based on the City of Torrance’s classification, effectively there are 2 types of streets: main streets and local streets. Main streets are those long, straight streets designed to accommodate traffic and some retail, and local streets are those neighborhood streets designed to host residential usage. This is consistent with post-WWII planning ideology in North America, and totally prevalent in Torrance as well. Despite this, space syntax measurements will still return a hierarchy of connections in the city based on gradations of centrality values. If we were to select streets based on these measurements to form the connections between the micro-centers, then surely the networks would be formed from a mix of freeways, main streets, and local streets.
While many other cities which demonstrate a hierarchical arrangement of spaces, this would be counterintuitive and counterproductive in Torrance. Even if a ‘local’ street has significance in the overall street network and has a higher centrality, it practically cannot become part of a larger movement network or strategy as it will always be used, considered, and retain the morphology of the local street, separate from higher speed traffic.

In summary, our micro-center strategy was developed to provide the most broad-scale and flexible strategy for development of any sort in Torrance. The strategy could form a template, and be expanded in greater detail, expanded, or extended to work on a larger scale. The process was to select micro-centers representing the points of overlap between the top 10% streets with the highest Choice, Integration, and Metric Mean Depth values. This was done at four radii to represent a broad range of different mobility-focused movement scales. These centers are linked together by a network derived from the overlapping segments falling in the top 10% of all Metric Choice and Integration measures.
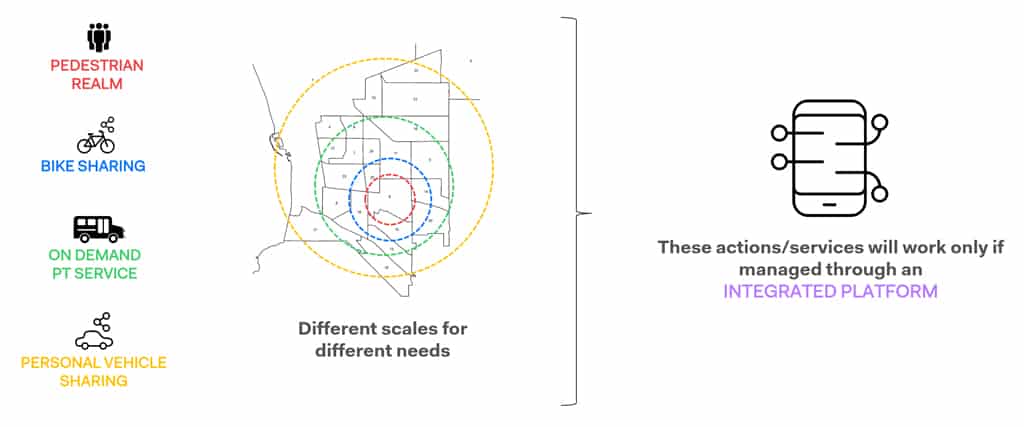
Depending on the radius at which the centrality emerged, several areas were identified as ideal locations for pilot projects and the installation of mobility services, from renovation of main pedestrian corridors, to bike sharing docks, to electric cars charging stations, to innovative bus shelter with real time information and possibility to request on-demand services.
Conclusions
In our general mobility study for Torrance, USA commencing in summer 2016, we employed space syntax spatial analysis in three ways. We used this in a preliminary, exploratory analysis to understand emerging patterns in Torrance and its regional context, and later compared these findings against the distinct and more familiar city of Milan, Italy. We next relied on centrality measures to make predictions about traffic flows in order to compare observed traffic patterns with that which would be expected if traffic flows followed intrinsic centrality hierarchies. Finally, we used spatial measures to identify local micro-centers and create a strategy for connecting them together in an effort to create a broad, comprehensive, and scalable strategy for any and all future works in Torrance.
The study opened up a reading of new relationships between Old Town Torrance and its adjacent cities that, at a Metric Mean Depth with radius of 5.0 km, started to form a new cluster that extends across administrative limits. It was hence observed that the cluster formed is less consolidated compared to others within the tested network, however it has the potential of being reinforced and of competing in scale, overcoming the socioeconomic, demographic and governance traits that currently impede the network from working as a coherent whole. This steered us in defining the interventions and identifying pilot projects that worked to enforce links between Old Town Torrance and its adjacent network in Carson City. The projects included improvements to the current public transport network, public transport new lines, on-demand mobility offering, improvements to walking conditions, etc. All interventions were designed, in terms of content and scale, to operate across legislative boundaries and to open dialogue between the two local administrations. Los Angeles City was also part of the dialogue as its administrative boundary oddly extends towards Long Beach separating the cities of Torrance and Carson through as strip of land of less than 900 meters wide. In brief, the apparently theoretical Mean Depth analysis that was launched with no predefined objectives opened up new ideas and underpinned a strong argument on the need and huge benefit in developing and launching projects at a larger scale, that looks at the territory beyond the administrative limits of cities and city fragments in Los Angeles’ urban continuum.
Our preliminary analysis gave us a strong start to the project, especially as we had difficulties reading the spatial, morphological, and functional use of Torrance through observation and experience alone, particularly due to its homogenous and unvarying density patterns, few historic areas, and commerce, retail, and land-use patterns that we could not explain readily, despite our large, experienced, and highly-diverse team of professionals. Our observations, and especially our quantitative comparison with Milan helped identify and explain the urban structure in Torrance, and especially the changing significance of the various scales of movement. One potent observation was that those streets (segments) which are significant at lower radii of centrality are not significant at larger radii; there is, in fact, minimal intelligibility in the system.
Again, the exercise was carried out at different radii and was showing the slope at which the angular integration decreases as the measurement radius increases in each of the cities. The difference in slope of the angular-integration-by-metric-radius curve between Torrance and Milan allowed us to identify a turning point at which the two curves meet, where Torrance started to ‘perform’ better at a radius of 5.0 km and above. This showed the inherent potentials a typical European city has in terms of walkability for distances that are less than 5.0 km versus a typically low-to-medium density city in LA which was planned and structured to cover longer distances. The regular grid showed also its potentials in connecting remote parts of the city versus the ring road which, beyond a certain travel distance, result to be less efficient. Despite this, different parts of the city still showed different results: Torrance showed some potentials in its Old Town to become a fully walkable neighborhood, despite suffering from being disconnected from the rest of its network due to open and empty industrial areas that separate the Old Town from other commercial and residential parts towards the western side of the city.
This exercise was beneficial for calibrating the mobility offering that we proposed as we attributed a sense of scale/ distance to internal movements. As 5.0 km is not considered a walkable distance, we had to devise solutions that focused on bicycle and scooter sharing schemes (at a time when the world was not producing 5000 scooters a day!), last-mile solutions at stops encouraging multimodal trips and other interventions that were tailored to the scale that we have learnt through using space syntax and cross-referencing case studies worldwide.
A broad range of alternative mobility solutions have been proposed to our Client for the entire City of Torrance, from renovation of main pedestrian corridors, to bike sharing docks, to electric cars charging stations, to innovative bus shelter with real time information and possibility to request on-demand services.
References
Dibble, J: ‘Urban Morphometrics: towards a quantitative science of urban form’. PhD thesis, University of Strathclyde, UK (2017)
Gower, J.C.: A General Coefficient of Similarity and Some of Its Properties. Biometrics, Vol. 27, No. 4., 857-871, (Dec., 1971)
Hillier, B., W. R. G., Yang, T. and Turner, A.: Normalising Least Angle Choice in Depthmap and How It Opens up New Perspectives on the Global and Local Analysis of City Space. Journal of Space Syntax, 3, 155-193 (2012)
Turner, A.: From axial to road-centre lines: a new representation for space syntax and a new model of route choice for transport network analysis. Environment and Planning B: Planning and Design 34(3), 539-555 (2007)